HOME ABOUT ME RESEARCH PUBLICATIONS TEACHING LAB
LINKS GALLERY
!-- Navbar on small screens -->

Research Interests

(1) Developing methods for the data-driven analysis and modeling of complex systems primarily using the theoretical frameworks of networks, nonlinear dynamics, and applied statistics.

(2) Mathematical and computational modeling of systems involving the interplay of networks, nonlinear and stochastic dynamics.

See below for brief descriptions of some of my research interests.
Data-Driven Analysis and Modeling

In my research, I have developed methods for the analysis of datasets originating from many different disciplines, and ranging from a few hundred points in a time series to massive spatiotemporal datasets. Two of my favorite theoretical tools for the data analysis-oriented problems are nonlinear time series analysis and the theory of complex networks.


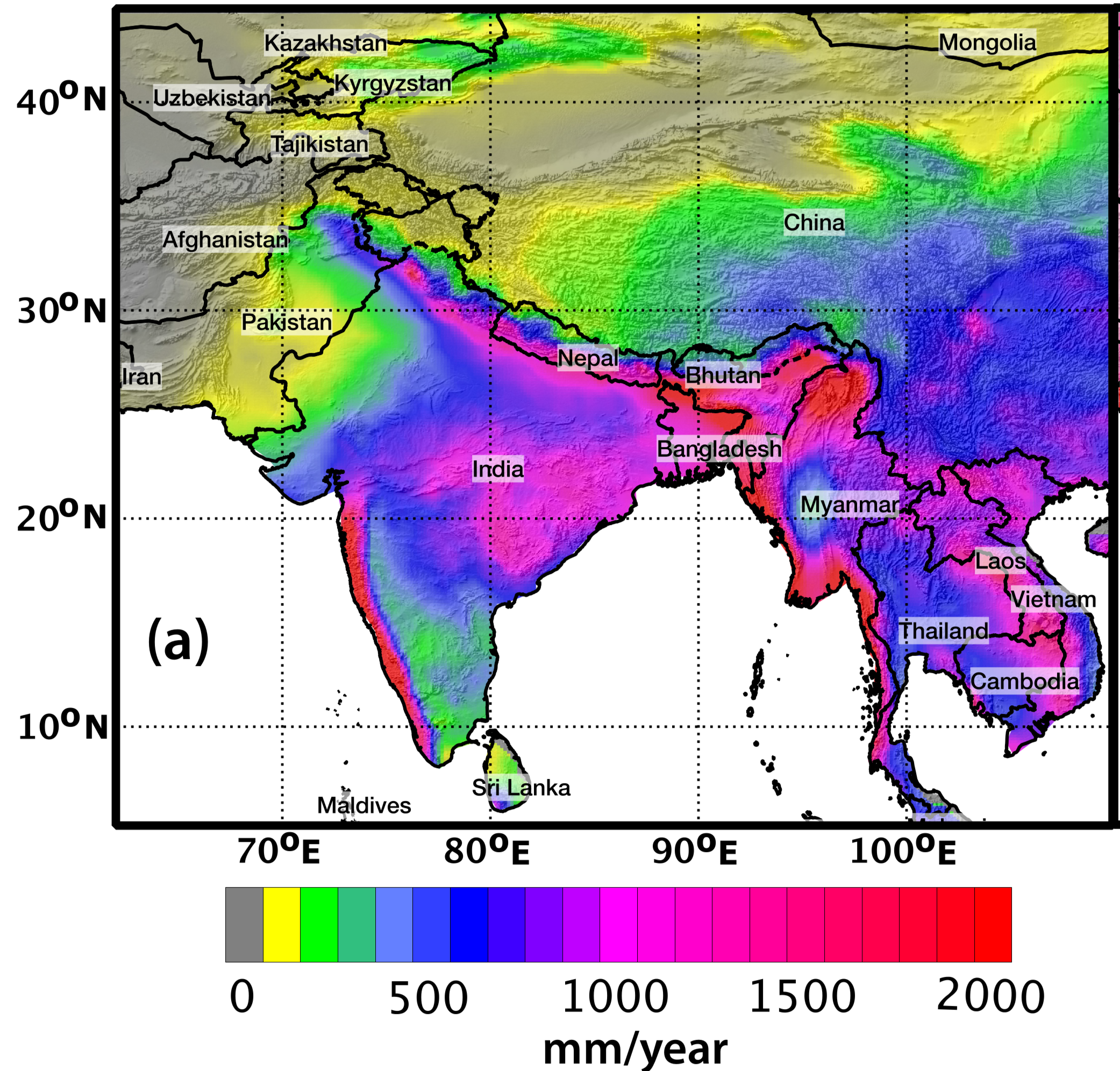
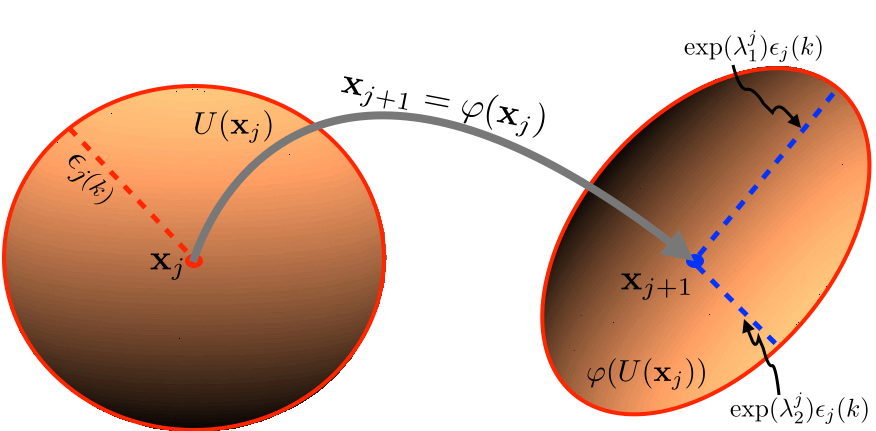Networks epitomize many real-world systems, where nodes represent different elements of a system, and edges represent connections between the elements. For example, the brain is a network of neurons; society consists of networks of people; the network of web pages is what we call the world wide web. The analysis of networks requires approaches drawn from many disciplines, and network science is the name given to the compilation of these approaches. The straightforward application of network science to problems in data analysis is when a given dataset contains information about relationships between objects or agents—for example, online social networks, or protein-protein interaction networks in biology. Another approach involving the application of network science to data analysis is when underlying networks can be inferred from spatiotemporal or image datasets, for example, in neuroscience using fMRI data. This approach is not only limited to cases where there is an underlying physical network but also includes instances where the existence of a network is a theoretical abstraction —for instance, climate networks or network representation of time series data. My research interests span both the above approaches.


Nonlinear time series analysis is the name given to the collection of tools which employ theories from nonlinear dynamical systems to solve problems in time series analysis. This discipline is on the interface of dynamical systems and data analysis. The underlying philosophy of nonlinear time series analysis is that nature is inherently nonlinear and dynamical and data coming from observing nature and its phenomena should be probed using the theories of nonlinear dynamics. My primary interest in nonlinear time series analysis is the following problem. Given a time series originating from a nonlinear dynamical system (most natural and social systems will satisfy this assumption); then how to identify and predict dynamical transitions (qualitative shifts in dynamics) and instabilities in this system without constructing an explicit mathematical model for it.


Visualization is the most powerful data analysis tool, creative visualization at times can provide profound insights into the data. The ever-increasing power of CPUs, graphics cards and the simultaneous revolution in graphing and imaging software packages have equipped researchers with exceptionally powerful visualization toolboxes. My exposure to visualization was first through my great fascination with patterns that emerge in computational simulations of nonlinear dynamical systems, especially the fractal generated using difference equations (like one on the left). More recent exposure to visualization is through many data analysis problems I have worked over the years, including mathematical tools such as recurrence plots (method for convert a time series data into a binary image), etc. I am always eager to learn and explore new Python or Matlab based visualization tools.


Extreme or rare events such as floods, droughts, cyclones, or forest fires are of massive socioeconomic significance. With changing climate an increase in frequency and variability of such events has been observed all over the planet. My interest is in understanding and characterizing the new emerging patterns in extreme precipitation/rainfall events over monsoonal regions of the world from historical climate data sets. Monsoons are not only among the most prominent and dynamic phenomena of the climate system manifesting over large parts of the tropics but also forms the lifeline of several regions of the world. It has been argued that the basic origin of the monsoons lies in the differential heating of the land and the sea during the summer season, which results in setting of a positive moisture advection feedback leading to widespread rainfall. The release of latent heat in the processes of precipitation over the land provides the feedback for maintaining this temperature gradient thus sustaining monsoonal circulation. One of the region of interest in my research has been South Asia, which receive roughly 80% of the total annual rainfall during summer monsoon months.

Mathematical and Computational Modeling
Mathematical and Computational Modeling

Complex systems are one of the most pervasive types of systems in nature and society. In most general case complex systems consist of three ingredients: nonlinearity, stochasticity, and intricate interactions among individual units of the systems. One of the primary challenges in modeling complex systems is the fact that nonlinear dynamical systems interacting through an intricate web of connections tend to behave differently than when observed as individual units. Hence, analytical tools used in the analysis of low dimensional nonlinear dynamical systems are of limited usefulness in studying complex systems. One of the significant development in studying complex systems has been the new science of Networks. Network theory provides the powerful mathematical framework to represent and analyze the intricate connections among individual units of a complex system. Another ubiquitous component in complex systems with far-reaching consequences is noise. A complete and accurate study of complex systems must take into account noise and include methods of stochastic processes in the analysis.


One problem within the realms of complex systems that excites me a lot is the role of network topology or structure in altering various types of dynamics, both in the noisy and noiseless environments. An answer to this problem can lead to a proper mathematical understanding of the effect of different macro and micro level network structures on nonlinear dynamical systems. In search of the answer, with my colleagues, I have modeled processes involved in the spread of biological and social contagions and noise-induced phenomena in networks. The most significant work I have done in this direction is the modeling of collective opinion formation on co-evolving networks. The dynamic model I have used for the purpose is the well-known voter model. In my work, I have shown that transitivity/clustering in a network can play a critical role in altering the dynamics of voter model simulated on a co-evolving network. I have also been attempting to use a similar model to analyze online social network data coming from Facebook and Twitter.

One of the phenomena encountered in a variety of physical, chemical, biological and engineering systems is synchronization: the emergence of coherent activity in a system of interacting dynamical units. Some well-known examples of synchronization phenomena include the synchronous flashing of fireflies, acoustic synchrony in snowy tree crickets, oscillatory patterns in Belousov- Zhabotinsky reaction, synchrony in predator-prey cycles etc. One of the disciplines where synchronization has attracted much attention is Neuroscience. There exists substantial empirical evidence that synchronization is the central mechanism in neuronal information processing. My interest in synchronization is in exploring the role of network topology (static or dynamic) in both deterministic and stochastic settings with applications to neuroscience.